Author
Làm thế nào để chúng ta biết là bài toán của chúng ta là phi tuyến (Nonlinearity)?
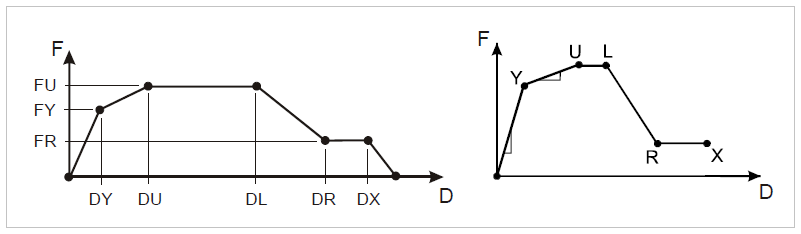
Có lẽ cách tốt nhất và thực tế nhất là nhìn vào mối quan hệ giữa tải trọng(LOAD) và chuyển vị(Displacement)
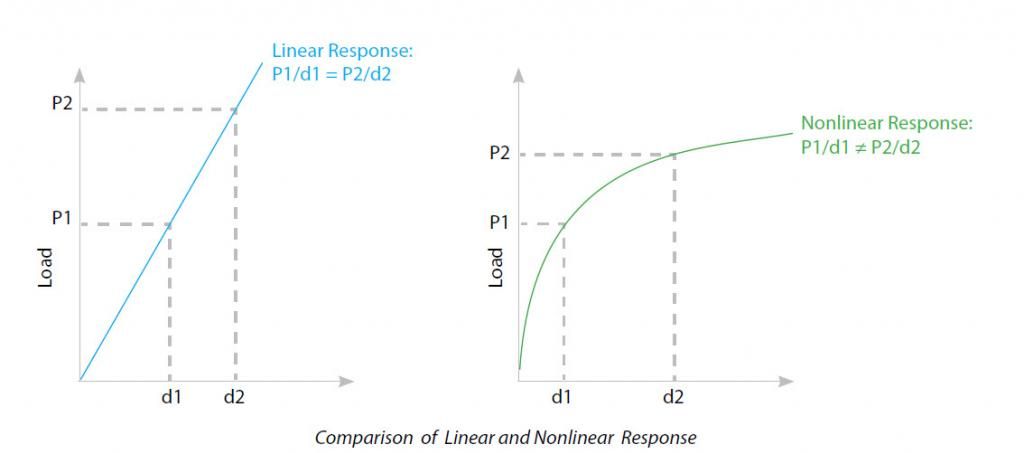
Như chúng ta đã biết, khi phản ứng của kết cấu(structure response = Deformation, stress, strain) tỷ lệ tuyến tính với tải trọng (LOAD = force, pressure, moment, temp, ...) thì khi đó bài toán là phân tích tuyến tính(Linear analysis).
Còn khi mối quan hệ giữa LOAD & RESPONSE không còn tỷ lệ với nhau nữa thì bài toán đó là phi tuyến.
Ví dụ: khi một kết cấu làm bằng thép chịu tải trọng (về độ lớn) tương đối thấp hơn so với độ bền của vật liệu có thể xấp xỉ coi bài toàn đó là tuyến tính tĩnh.
Tuy nhiên, trong hầu hết trường hợp, ứng xử của vật liệu là không tuyến tính trong khi làm việc hoặc hình học của kết cấu làm cho nó không còn RESPONSE tuyến tính.
Vì lý do chi phí và ưu thế về khối lượng của vật liệu phi kim loại (nonmetal: polymers, woods, composites), vật liệu phi kim loại đang được thay thế trong rất nhiều ứng dụng.
Bên cạnh đó vì giới hạn của nguồn tài nguyên, các kết cấu cần được tối ưu hoá để cho tối ưu bền nhất có thể, dẫn đến khá gần với độ bền của vật liệu và khi đó kết cấu bắt đầu ứng xử phi tuyến.
***) Linear static v.s Nonlinear static
Như chúng ta đã biết, ma trận độ cứng liên quan đến LOAD (F) và Response (Deformation, stress, strain) được giả thiết là hằng số cho bài toán tĩnh. Tuy nhiên trong thực tế kết cấu thực thường ứng xử phi tuyến.
Công thưc tính ma trận độ cứng bao gồm các thông số hình học (chiều dài<length>, diện tích mặt cắt ngang và mô men quán tính) và đặc tính vật liệu (mô đun đàn hồi, ...).
Bài toán tuyến tính tĩnh sẽ giải thiết rằng các thông số này không thay đổi khi đặt tải trọng vào. Còn Bài toán phi tuyến tĩnh sẽ tính đến việc thay đổi những thông số này. Để đạt được những thông số này trong phân tích, sẽ cần sẽ phải tính lại ma trận độ cứng ứng với kết cấu đã thay đổi mỗi khi tăng lực đặt vào.
Mặc dù thực tế hầu hết là phi tuyến nhưng trong rất nhiều trường hợp, có thể giả thiết gần đúng là tuyến tính. Ngoài ra dưới góc nhìn về hiệu năng tính toán của máy tính, tuyến tính sẽ tiết kiếm chi phí hơn (vì phi tuyến luôn phải tính lại ma trận độ cứng ứng với mỗi thay đổi)...
Từ các khái niệm cơ bản liên quan đến phi tuyến ở trên, người ta chi bài toán phi tuyến thành 3 loại chính.
1. Phi tuyến hình học (Geometric nonlinearities)
Phi tuyến hình học liên quan đến : Large Strain, Large rotation, Large deformation
Bài toán phi tuyến hình học sẽ xem xét đến mặt cắt ngang hình học bị thay đổi do biến dạng lớn (large deformation). Nhắc lại, trong bài toán tuyến tính tĩnh, mặt cắt ngang coi như là const.
Hoặc bài toán chuyển vị lớn (large displacement) trong hiện tượng buckling(kết cấu membrain bị phá huỷ đột ngột vì ứng suất nén cao (high compressive stress) mặc dù ứng suất này thấp hơn ứng suất phá huỷ của vật liệu.
Như vậy phi tuyến hình học có thể chia làm 2 loại:
a) Large displacement, rotations (small strain, linear or nonlinear material)
b) Large displacement, rotations, large strain
2. Vật liệu phi tuyến (Material nonlinearity)
a) Nonlinear Elastic (vượt qua E trên đường cong stress-strain của vật liệu kim loại) => Ứng dụng trong ngành công nghiệp oto, hàng không, tàu thuỷ.
b) Non metal (plastic)
c) Hyperelastic: (Cao su: có khả năng chịu biến dạng rất lớn) >> ứng dụng trong Gasket
(cần các cao thủ bổ xung giải thích rõ hơn mục này)
3. Contact nonlinearity
- Ví dụ mô phỏng tiếp xúc vật lý giữa 2 chi tiết: chẳng hạn giữa trục và vòng bi, hoặc press fit giữa 2 cylinder.
Có lẽ cách tốt nhất và thực tế nhất là nhìn vào mối quan hệ giữa tải trọng(LOAD) và chuyển vị(Displacement)
Như chúng ta đã biết, khi phản ứng của kết cấu(structure response = Deformation, stress, strain) tỷ lệ tuyến tính với tải trọng (LOAD = force, pressure, moment, temp, ...) thì khi đó bài toán là phân tích tuyến tính(Linear analysis).
Còn khi mối quan hệ giữa LOAD & RESPONSE không còn tỷ lệ với nhau nữa thì bài toán đó là phi tuyến.
Ví dụ: khi một kết cấu làm bằng thép chịu tải trọng (về độ lớn) tương đối thấp hơn so với độ bền của vật liệu có thể xấp xỉ coi bài toàn đó là tuyến tính tĩnh.
Tuy nhiên, trong hầu hết trường hợp, ứng xử của vật liệu là không tuyến tính trong khi làm việc hoặc hình học của kết cấu làm cho nó không còn RESPONSE tuyến tính.
Vì lý do chi phí và ưu thế về khối lượng của vật liệu phi kim loại (nonmetal: polymers, woods, composites), vật liệu phi kim loại đang được thay thế trong rất nhiều ứng dụng.
Bên cạnh đó vì giới hạn của nguồn tài nguyên, các kết cấu cần được tối ưu hoá để cho tối ưu bền nhất có thể, dẫn đến khá gần với độ bền của vật liệu và khi đó kết cấu bắt đầu ứng xử phi tuyến.

***) Linear static v.s Nonlinear static
Như chúng ta đã biết, ma trận độ cứng liên quan đến LOAD (F) và Response (Deformation, stress, strain) được giả thiết là hằng số cho bài toán tĩnh. Tuy nhiên trong thực tế kết cấu thực thường ứng xử phi tuyến.
Công thưc tính ma trận độ cứng bao gồm các thông số hình học (chiều dài<length>, diện tích mặt cắt ngang và mô men quán tính) và đặc tính vật liệu (mô đun đàn hồi, ...).
Bài toán tuyến tính tĩnh sẽ giải thiết rằng các thông số này không thay đổi khi đặt tải trọng vào. Còn Bài toán phi tuyến tĩnh sẽ tính đến việc thay đổi những thông số này. Để đạt được những thông số này trong phân tích, sẽ cần sẽ phải tính lại ma trận độ cứng ứng với kết cấu đã thay đổi mỗi khi tăng lực đặt vào.
Mặc dù thực tế hầu hết là phi tuyến nhưng trong rất nhiều trường hợp, có thể giả thiết gần đúng là tuyến tính. Ngoài ra dưới góc nhìn về hiệu năng tính toán của máy tính, tuyến tính sẽ tiết kiếm chi phí hơn (vì phi tuyến luôn phải tính lại ma trận độ cứng ứng với mỗi thay đổi)...
Từ các khái niệm cơ bản liên quan đến phi tuyến ở trên, người ta chi bài toán phi tuyến thành 3 loại chính.
1. Phi tuyến hình học (Geometric nonlinearities)
Phi tuyến hình học liên quan đến : Large Strain, Large rotation, Large deformation
Bài toán phi tuyến hình học sẽ xem xét đến mặt cắt ngang hình học bị thay đổi do biến dạng lớn (large deformation). Nhắc lại, trong bài toán tuyến tính tĩnh, mặt cắt ngang coi như là const.
Hoặc bài toán chuyển vị lớn (large displacement) trong hiện tượng buckling(kết cấu membrain bị phá huỷ đột ngột vì ứng suất nén cao (high compressive stress) mặc dù ứng suất này thấp hơn ứng suất phá huỷ của vật liệu.
Như vậy phi tuyến hình học có thể chia làm 2 loại:
a) Large displacement, rotations (small strain, linear or nonlinear material)
b) Large displacement, rotations, large strain
2. Vật liệu phi tuyến (Material nonlinearity)
a) Nonlinear Elastic (vượt qua E trên đường cong stress-strain của vật liệu kim loại) => Ứng dụng trong ngành công nghiệp oto, hàng không, tàu thuỷ.
b) Non metal (plastic)
c) Hyperelastic: (Cao su: có khả năng chịu biến dạng rất lớn) >> ứng dụng trong Gasket
(cần các cao thủ bổ xung giải thích rõ hơn mục này)
3. Contact nonlinearity
- Ví dụ mô phỏng tiếp xúc vật lý giữa 2 chi tiết: chẳng hạn giữa trục và vòng bi, hoặc press fit giữa 2 cylinder.