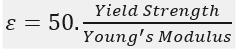Author
Em xin chào các bác ạ, xin phép được xưng em.
Hôm nay em xin phép được chia sẻ về một số thông tin mà em đã học được dưới tư cách là một sinh viên. Em cũng không chắc chắn được những thông tin này đúng hay sai, nên là rất mong các tiền bối có thể cho em nhận xét và thêm "gạch đá" để xây nhà ạ. Em sẽ còn cập nhật thêm nữa.
Để đánh giá kết quả CAE không hề đơn giản. Ngay cả khi bài toán mô phỏng cho ra một giá trị “bảy sắc cầu vồng” nhìn rất đẹp, bạn vẫn cần phải quyết định kết quả đó có đúng hay không.
Em sẽ lấy một ví dụ đơn giản
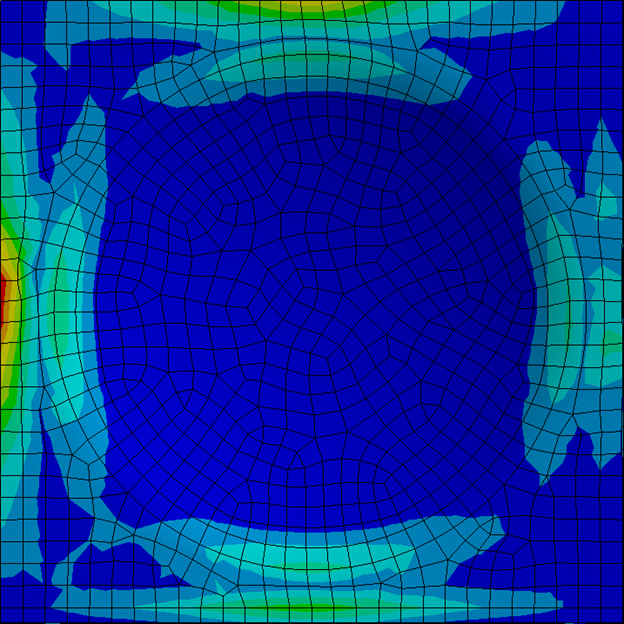
Thường thì sau khi bộ giải cho kết quả, em sẽ nhìn vào kết quả Von-Mises stress đầu tiên. Cũng đúng thôi, vì nó là thước đo tốt nhất để đánh giá “sự phá hủy” của chi tiết mà. Nhưng làm thế nào để đánh giá được kết quả đó đúng hay sai?
Đánh giá giá trị Von-Mises stress
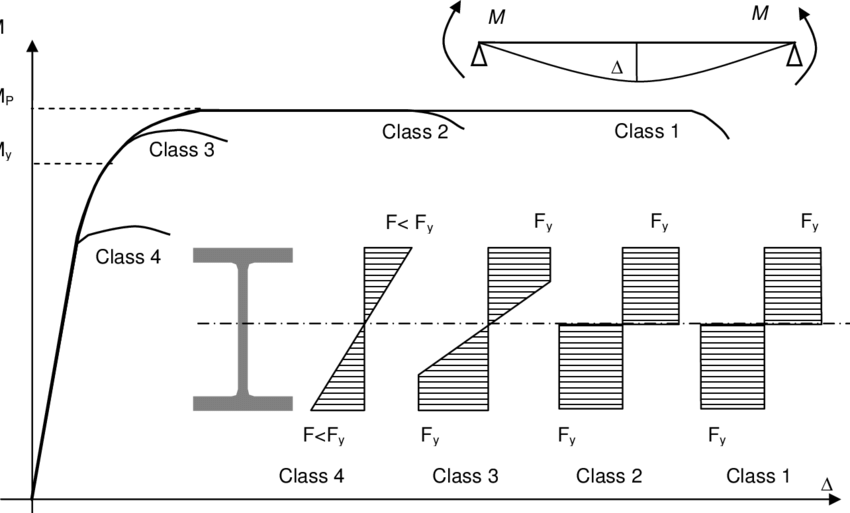
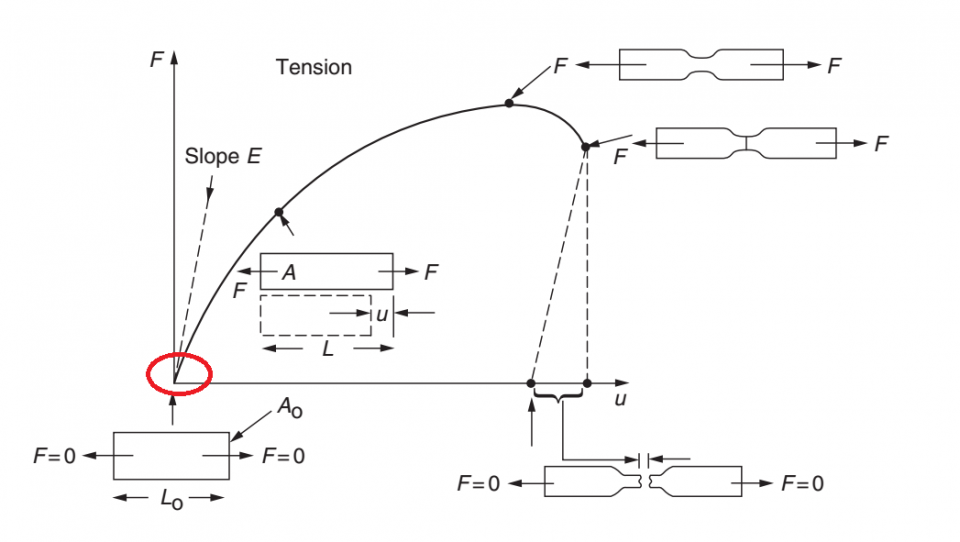
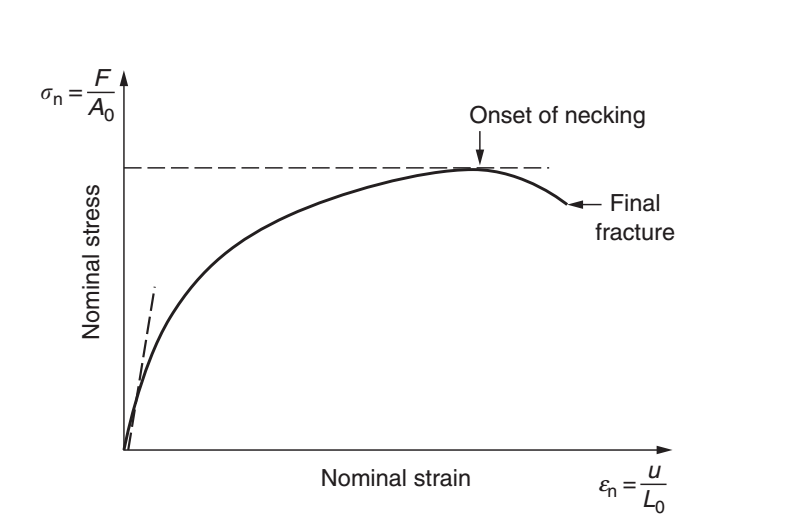
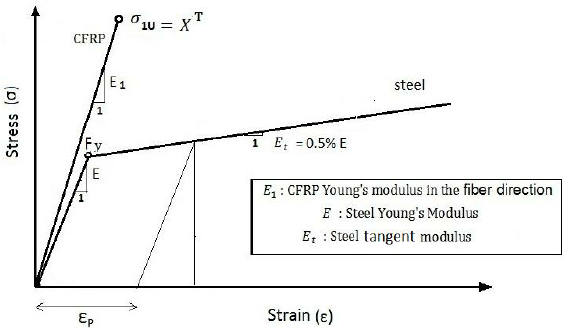
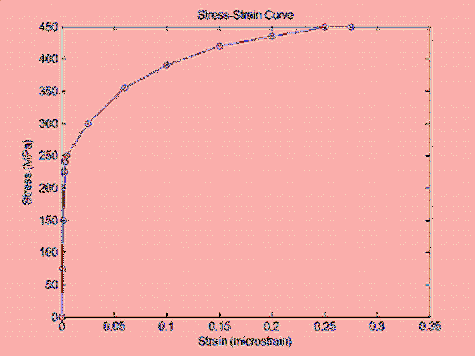
Khi kết quả Von-Mises stress nhỏ hơn Yield strength thì có nghĩa là kết quả đó có thể tin tưởng được. Tuy nhiên có nhiều khả năng sẽ nhận được là kết quả sẽ lớn hơn Yield strength, khi đó hãy kiểm tra biểu đồ Stress-Strain của vật liệu.
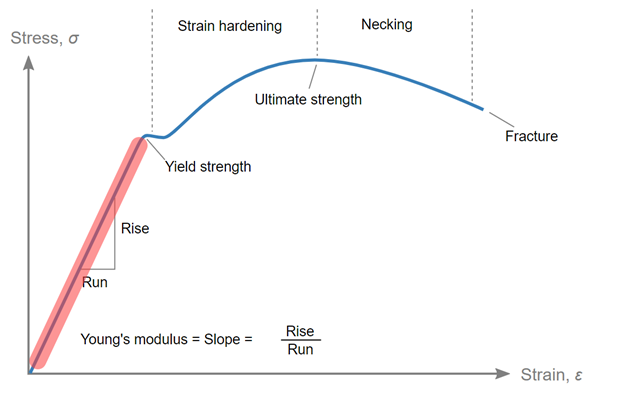
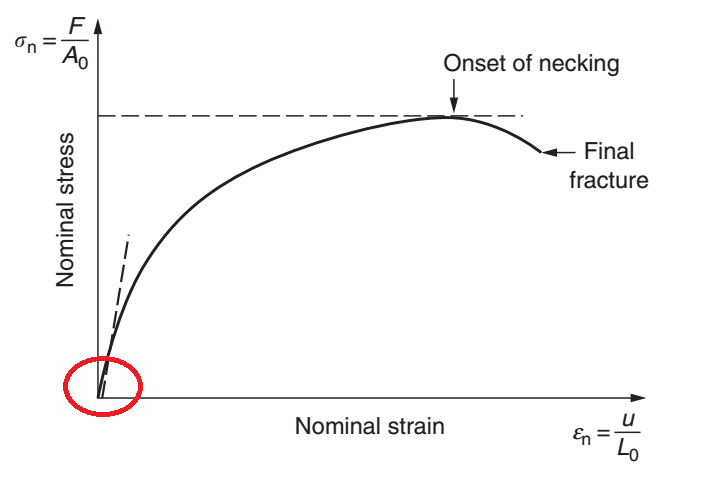
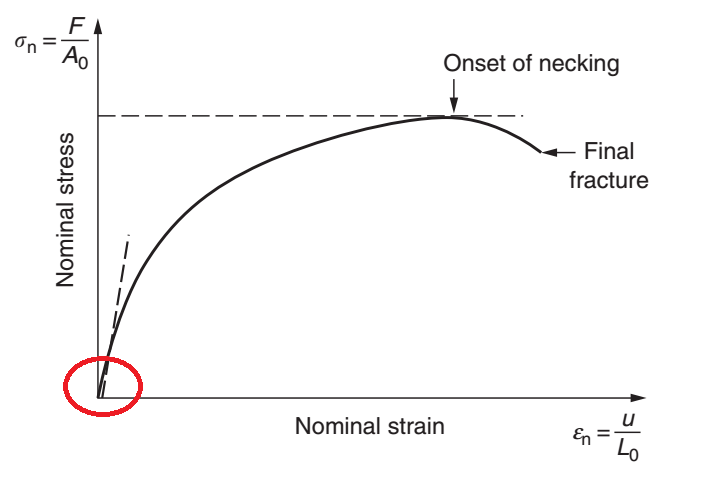
Trong phần được tô đỏ, giả định phân tích tuyến tính được áp dụng, nghĩa là mọi thứ đang hoạt động tốt. Nhưng khi biến dạng nằm ngoài vùng tuyến tính, bộ giải vẫn đang cố gắng áp dụng giả định này vào thuật giải khiến cho kết quả stress cao hơn rất nhiều so với Yield strength, thậm chí còn lớn hơn hàng chục lần
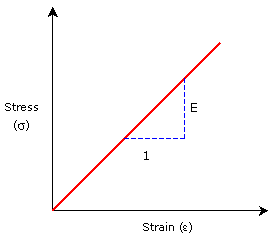
Stress lớn hơn Yield strength không có nghĩa là kết cấu đó thất bại
Em hay gặp trường hợp một số khu vực rất nhỏ trên chi tiết có stress cao hơn giới hạn. Những vùng nhỏ đó có stress lớn hơn Yield strength không có nghĩa là thất bại, vấn đề này có thể do “FEA error” gây ra. Khi đó cần phải giải quyết thế nào???
Sử dụng Nonlinear Material
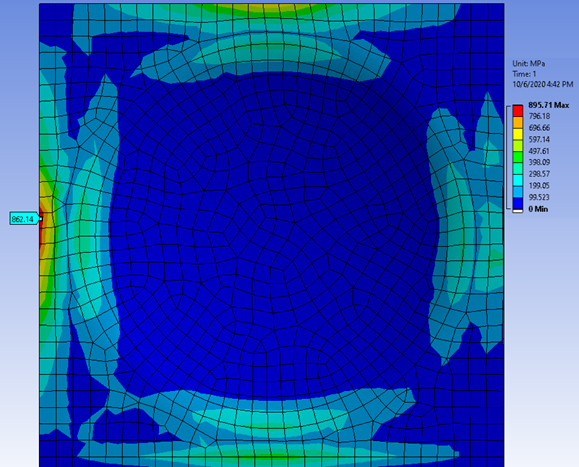
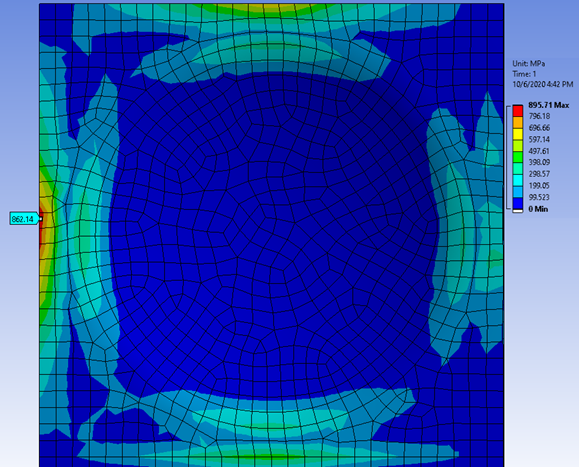
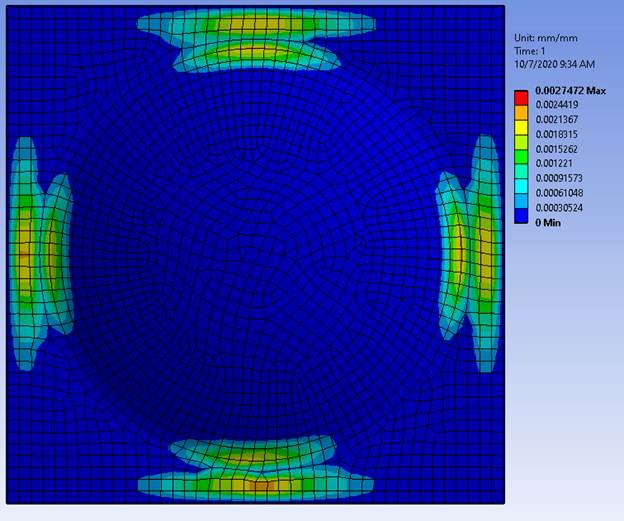
Sử dụng đặc tính của vật liệu phi tuyến là một cách để hỗ trợ giải quyết vấn đề Stress quá cao. Hai hình ảnh minh họa, hình trên sử dụng giả định tuyến tính, hình dưới là phi tuyến, em đã thấy có sự thay đổi rõ ràng về kết quả.
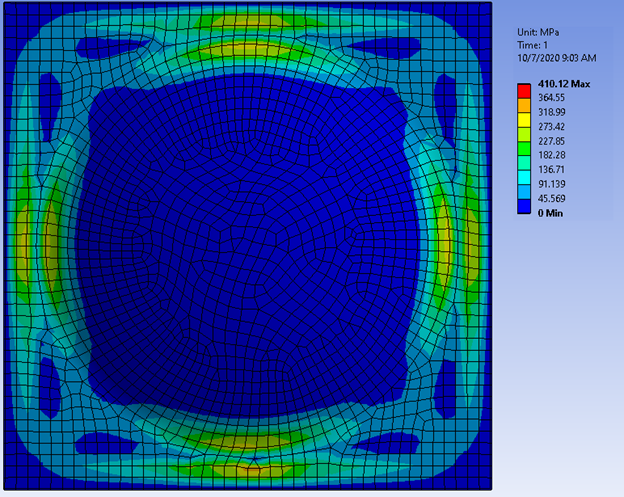
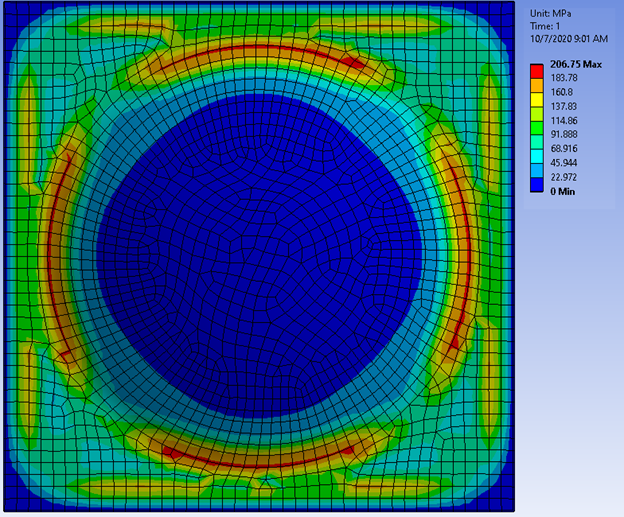
Có khá nhiều cách để sử dụng đặc tính vật liệu phi tuyến, đơn giản nhất là em sử dụng Bi-linear.
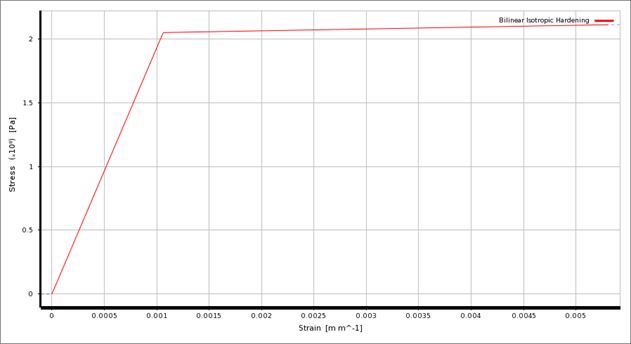
Độ biến dạng tương đối (Plastic Strain) có thể chấp nhận được trong mô hình này được xác định theo công thức ε=50.(Yield strength / Young's Modulus) (rơi vào khoảng 5% đối với Stainless steel). Dựa vào đó đó em có thể biết được kết quả của mô hình này đúng hay sai
Một số nguồn tham khảo:
- https://www.wikipedia.org/
- http://www.materials.unsw.edu.au/tutorials/online-tutorials
- https://www.phd.eng.br/wp-content/uploads/2015/12/en.1993.1.6.2007.pdf
Hôm nay em xin phép được chia sẻ về một số thông tin mà em đã học được dưới tư cách là một sinh viên. Em cũng không chắc chắn được những thông tin này đúng hay sai, nên là rất mong các tiền bối có thể cho em nhận xét và thêm "gạch đá" để xây nhà ạ. Em sẽ còn cập nhật thêm nữa.
Để đánh giá kết quả CAE không hề đơn giản. Ngay cả khi bài toán mô phỏng cho ra một giá trị “bảy sắc cầu vồng” nhìn rất đẹp, bạn vẫn cần phải quyết định kết quả đó có đúng hay không.
Em sẽ lấy một ví dụ đơn giản

Thường thì sau khi bộ giải cho kết quả, em sẽ nhìn vào kết quả Von-Mises stress đầu tiên. Cũng đúng thôi, vì nó là thước đo tốt nhất để đánh giá “sự phá hủy” của chi tiết mà. Nhưng làm thế nào để đánh giá được kết quả đó đúng hay sai?
Đánh giá giá trị Von-Mises stress
Khi kết quả Von-Mises stress nhỏ hơn Yield strength thì có nghĩa là kết quả đó có thể tin tưởng được. Tuy nhiên có nhiều khả năng sẽ nhận được là kết quả sẽ lớn hơn Yield strength, khi đó hãy kiểm tra biểu đồ Stress-Strain của vật liệu.

Trong phần được tô đỏ, giả định phân tích tuyến tính được áp dụng, nghĩa là mọi thứ đang hoạt động tốt. Nhưng khi biến dạng nằm ngoài vùng tuyến tính, bộ giải vẫn đang cố gắng áp dụng giả định này vào thuật giải khiến cho kết quả stress cao hơn rất nhiều so với Yield strength, thậm chí còn lớn hơn hàng chục lần

Stress lớn hơn Yield strength không có nghĩa là kết cấu đó thất bại
Em hay gặp trường hợp một số khu vực rất nhỏ trên chi tiết có stress cao hơn giới hạn. Những vùng nhỏ đó có stress lớn hơn Yield strength không có nghĩa là thất bại, vấn đề này có thể do “FEA error” gây ra. Khi đó cần phải giải quyết thế nào???
Sử dụng Nonlinear Material
Sử dụng đặc tính của vật liệu phi tuyến là một cách để hỗ trợ giải quyết vấn đề Stress quá cao. Hai hình ảnh minh họa, hình trên sử dụng giả định tuyến tính, hình dưới là phi tuyến, em đã thấy có sự thay đổi rõ ràng về kết quả.


Có khá nhiều cách để sử dụng đặc tính vật liệu phi tuyến, đơn giản nhất là em sử dụng Bi-linear.

Độ biến dạng tương đối (Plastic Strain) có thể chấp nhận được trong mô hình này được xác định theo công thức ε=50.(Yield strength / Young's Modulus) (rơi vào khoảng 5% đối với Stainless steel). Dựa vào đó đó em có thể biết được kết quả của mô hình này đúng hay sai

Một số nguồn tham khảo:
- https://www.wikipedia.org/
- http://www.materials.unsw.edu.au/tutorials/online-tutorials
- https://www.phd.eng.br/wp-content/uploads/2015/12/en.1993.1.6.2007.pdf
Attachments
-
280,4 KB Lượt xem: 56
-
280,4 KB Lượt xem: 65
-
3,1 KB Lượt xem: 79
Last edited: